RedBlackTree I

 |  WORDS: 660 | Time: 4 Mins
Data StructureTree
C++, Data Structure, Tree

RedBlackTree I Chinese version address

Binary Tree Review

There are several features of binary tree:

  1. if the left subtree of any nodes is not null, the value of all nodes on the left subtree is less than the value of its root node.
  2. if the right subtree of any nodes is not null, the value of all nodes on the right subtree is greater than the value of its root node.
  3. the left and right subtrees of any node are also binary tree.
  4. No nodes with equal values

Red Black Tree Overview

Red Black Tree is a special binary tree. each node of a red black tree has a bit to represenet the color, which can be red or black.

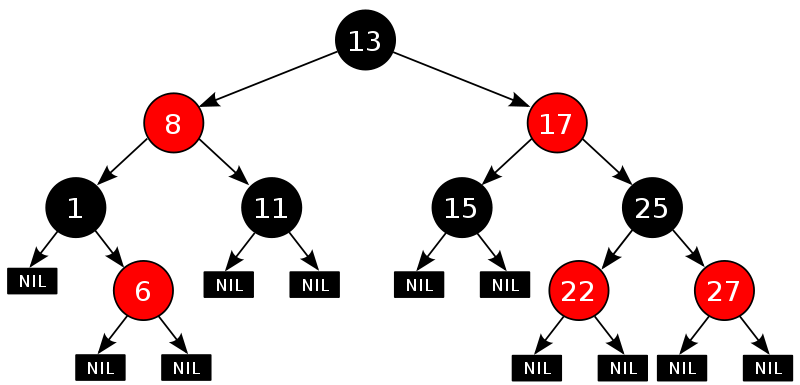
Red Black Tree Features

  1. the color of each node is red or black.
  2. the color of root node is black.
  3. the color of each leaf node is black.
  4. if a node is red, the subnode of it must be black.
  5. The same number of black nodes is included on all paths from a node to the node’s descendant node.

RedBlackTree

Notes:

  1. leaf node is means which node is null.
  2. Feature 5 to ensure that no path is twice as long as the other path. Thus, the red black tree is a relatively balanced binary tree.

Application of red black trees

The application of the red-black tree is particularly extensive, mainly because it uses it to store ordered data. Its time complexity is O (lgn), which is very efficient.

But its implementation is complicated, and insert, delete operation will pay more cost.

  • Set and Map in STL
  • TreeSet and TreeMap in Java
  • Virtual memory management in Linux

Basic operation of red black trees

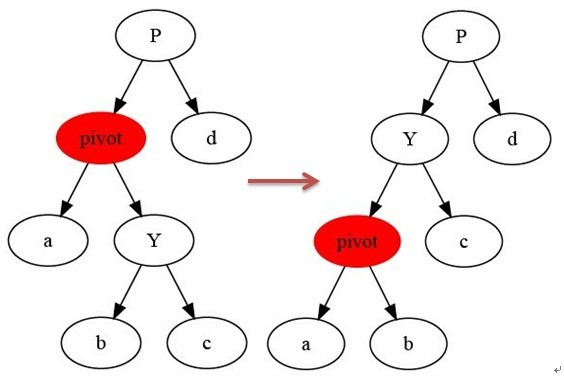
Left Rotation

1
2
3
4
5
                              z
  x                          /                  
 / \      --(左旋)-->        x
y   z                      /
                          y

Make left rotation on x node, and it will be a left node.

Left Rotate

Pseudo code

1
2
3
4
5
6
7
8
9
10
11
12
LEFT-ROTATE(T, x)  
 y ← right[x]            
 right[x] ← left[y]      
 p[left[y]] ← x         
 p[y] ← p[x]             
 if p[x] = nil[T]       
 then root[T] ← y                 
 else if x = left[p[x]]  
           then left[p[x]] ← y   
           else right[p[x]] ← y  
 left[y] ← x             
 p[x] ← y

C++ Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
template <class T>
void RedBlackTree<T>::leftRotate(RedBlackNode<T> *&root, RedBlackNode<T> *x) {

	RedBlackNode<T> *y = x->pRight;     

	x->pRight = y->pLeft;                    
	if(y->pLeft != nullptr) {
		y->pLeft->pParent = x;        
	}

	y->pParent = x->pParent;         

	if(x->pParent == nullptr) {      
		root = y;                      
	}
	else {
		if(x->pParent->pLeft == x) {    
			x->pParent->pLeft = y;      
		}
		else {
			x->pParent->pRight = y; 
		}
	}
	y->pLeft = x;                   
	x->pParent = y;                    
}

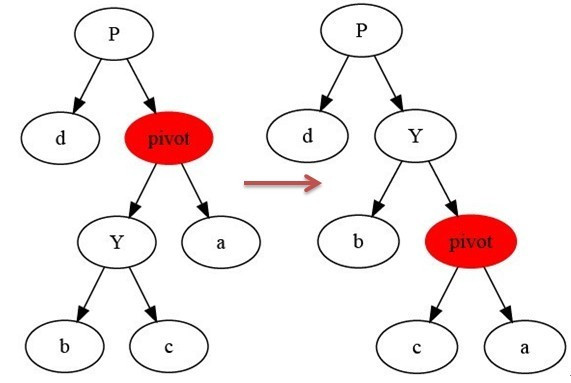
Right Rotation

1
2
3
4
5
                             y
  x                           \                 
 / \      --(右旋)-->           x
y   z                            \
                                  z

Make right rotation on x node, and it will be a right node.

Pseudo code

1
2
3
4
5
6
7
8
9
10
11
12
RIGHT-ROTATE(T, y)  
 x ← left[y]             
 left[y] ← right[x]      
 p[right[x]] ← y         
 p[x] ← p[y]             
 if p[y] = nil[T]       
 then root[T] ← x               
 else if y = right[p[y]]  
           then right[p[y]] ← x   
           else left[p[y]] ← x   
 right[x] ← y            
 p[y] ← x

C++ Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
template <class T>
void RedBlackTree<T>::rightRotate(RedBlackNode<T> *&root, RedBlackNode<T> *y) {

	RedBlackNode<T> *x = y->pLeft;    

	y->pLeft = x->pRight;              
	if(x->pRight != nullptr) {
		x->pRight->pParent = y;     
	}

	x->pParent = y->pParent;           

	if(y->pParent == nullptr) {        
		root = x;                       
	}
	else {
		if(y->pParent->pRight == y) {   
			y->pParent->pRight = x;     
		}
		else {
			y->pParent->pLeft = x;   
		}
	}

	x->pRight = y;       
	y->pParent = x;  
}

The Next Section

Share