Basic Graph Theory Chinese version address
Graph Theory
The definition of graph
The graph is composed of some points and the connection between these points. points are often called vertices, and the lines between points are called edges. It is usually written as G = (V,E).
Types of Graphs
According to whether the direction of the edge, the graph can be divided into: undirected and directed graph.
Undirected graph

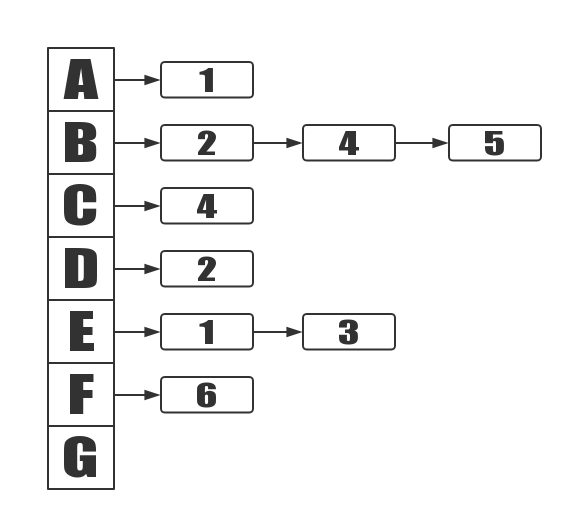
The above graph is an undirected graph, and all the edges of the undirected graph are not directed. It is written as G0=(V1,{E1}).
V1 = { A,B,C,D,E,F }
V1 represents a set of vertices composed of A, B, C, D, E, F.
E1 = { (A,B),(A,C),(B,C),(B,E),(B,F),(C,F),(C,D),(E,F),(C,E)}
E1 is by the edge (A, B), the edge (A, C)… And so on, and so on. (A, C) represents the edge that is connected by the vertex A and the vertex C.
Directed graph
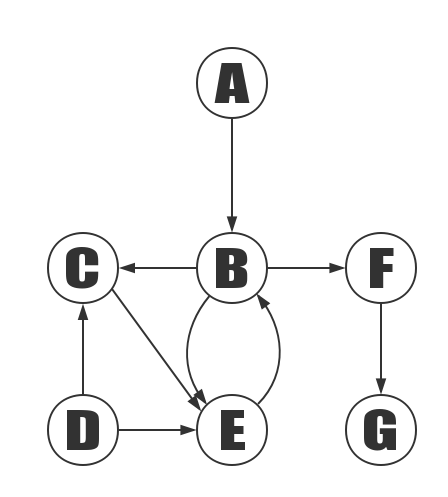
The graph above is a directed graph. Unlike an undirected graph, all the edges of the directed graph are directed. It is written as G2= (V2, {E2}).
V2={ A,C,B,F,D,E,G }
V2 represents a set of vertices composed of A, B, C, D, E, F, G.
E2={ <A,B>,<B,C>,<B,F>,<B,E>,<C,E>,<E,D>,<D,C>,<E,B>,<F,G> }
E2 is a
Adjacent & Degree
Adjacent
The two vertices on an edge are called the adjacency points.
For example, the vertex A and the vertex C in the above undirected graph are the adjacency points.
In the digraph, except for the adjoining points; there are also the notions of "In-Edge" and "Out-Edge".
In-Edge is means which edge that end with the vertex.
Out-Edge is means which edge that start with the vertex.
For example, the B and E in graph G2 are adjacent points;
Degree
In an undirected graph, the degree of a vertex is the number of edges adjacent to the vertex.
For example, the degree of the vertex A in the above undirected graph is 2.
In the digraph, there are also the notions of "In-Degree" and "Out-Degree"
In-Degree is means the number of edges at the end of the vertex.
Out-Degree is means the number of edges at the start of the vertex.
Degree of vertex = In-Degree + Out-Degree
Path & Circuit
Path: If a vertex sequence exists between the vertex (Vm) to the vertex (Vn). It means that Vm to Vn is a path
Length of path: the number of edge in this path.
Simple path: If the vertex of a path does not repeat, it is a simple path.
Circuit: If the first vertex of the path is the same as the last vertex, it is a Circuit.
Simple circuit: If the vertex of a circuit does not repeat, it is a simple circuit.
Connected graphs and connected components
Connected graph: For an undirected graph, there is an undirected path between any two vertices, and the undirected graph is called a connected graph.
strongly connected graph: For a directed graph, if there is a directed path between any two vertices in the graph, the directed graph is called a strongly connected graph.
Weight of Graph
This is special value in Huffman tree, it is means the value of a edge.
Graph Storage Structures
The storage structure of a graph is commonly used as adjacency matrix and adjacency list.
Adjacency Matrix
The adjacency matrix refers to the representation of a graph by a matrix. It uses a matrix to describe the relationship between the vertices of the graph (and the right of the arcs or edges).
Two arrays are usually used to implement the graph’s adjacency matrix: a one-dimensional array for storing vertex information and a two-dimensional array for saving edge information.
The disadvantage of adjacency matrix is more space-consuming.
Assuming that the number of vertices in the graph is n, the adjacency matrix is defined as:
A[i][j] = 0 is means that there is no edge.
A[i][j] = 1 is means that there are edge.
The following undirected graph:

The adjacency matrix of this undirected graph is as follows:
| N/A | A | B | C | D | E | F | G |
|---|---|---|---|---|---|---|---|
| A | 0 | 0 | 1 | 1 | 0 | 1 | 0 |
| B | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| C | 1 | 1 | 0 | 1 | 0 | 0 | 0 |
| D | 1 | 0 | 1 | 0 | 0 | 0 | 0 |
| E | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| F | 1 | 0 | 0 | 0 | 0 | 0 | 1 |
| G | 0 | 0 | 0 | 0 | 1 | 1 | 0 |
The following directed graph:

The adjacency matrix of this directed graph is as follows:
| N/A | A | B | C | D | E | F | G |
|---|---|---|---|---|---|---|---|
| A | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| B | 0 | 0 | 1 | 0 | 1 | 1 | 0 |
| C | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| D | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| E | 0 | 1 | 0 | 1 | 0 | 0 | 1 |
| F | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| G | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Adjacency List
The adjacency list is a chain storage representation method of a graph. It is an improved “adjacency matrix”, its disadvantage is that it is inconvenient to judge whether there is an edge between the two vertices, but it is less space relative to the adjacency matrix.
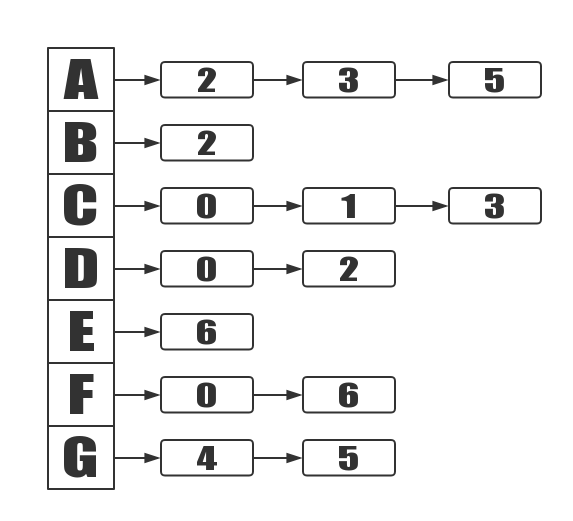
The following undirected graph:

The adjacency list of this undirected graph is as follows:
The following directed graph:

The adjacency list of this directed graph is as follows: