Topological Sort

 |  WORDS: 484 | Time: 3 Mins
AlgorithmSort
Algorithm, C++, Graph

Topological Sort Chinese version address

Topological Sort

Overview

Topological sorting means ordering a Directed Acyclic Graph(DAG) to get an ordered linear sequence.

In this way, it may be understood more abstractly.

For example, a project consists of four subsections A, B, C, and D, and A depends on B and D. C depends on D. Now to develop a plan to write A, B, C, D the order of execution. At this point, you can use topological sorting, which is used to determine the order in which things happen.

In topological sorting, if there is a path from the vertex A to the vertex B, B appears behind the A in the ranking result.

Algorithm Introduction

  1. Create a queue Q and a topological ordered result queue T.
  2. Put all the nodes that do not depend on the vertex in the Q.
  3. When Q has vertices, perform the following steps.
    1. Take a vertex n from Q (delete n from Q) and put it in T (add n to the result set).
    2. For every adjacent point m (n is the starting point and m is the ending point).
      1. Remove the edge (n, m).
      2. If m does not depend on the vertex, put b into Q.

The vertex A does not depend on the vertex, which means there is no edge to the end of the A.

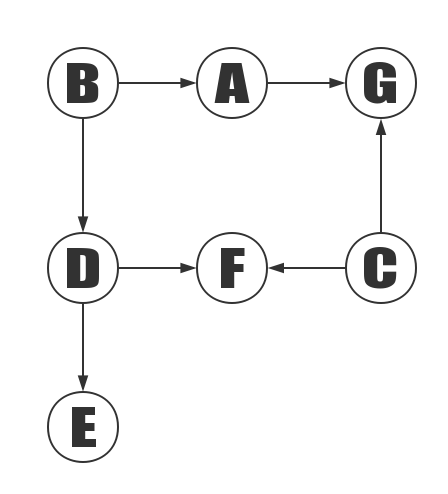
Sample Graph

The above diagram is an example of a demonstration of the topological sort.

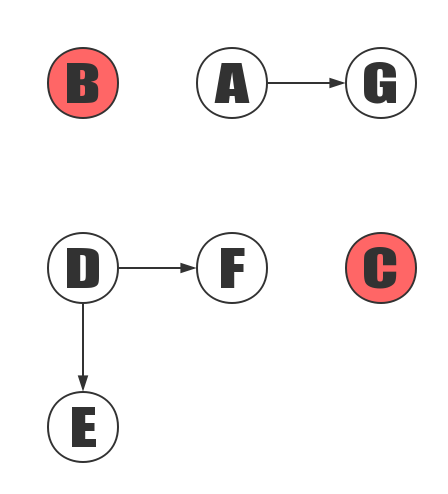
Step One

Step Two

Step Three

  1. Add B and C to the sorting result.

    Vertex B and vertex C are not dependent on the vertices, so C and C added to the result set T. Suppose ABCDEFG is stored sequentially, so visit B first and then C again. After accessing B, remove the edges (B, A) and (B, D) and add A and D to the queue Q. Similarly, remove the edges (C, F) and (C, G) and add F and G to Q.

    Add B to the sorted result, and then remove the edges (B, A) and (B, D); at this point, since A and D do not depend on vertices, add A and D to queue Q.

    The C is added to the sorting result, then the edge (C, F) and (C, G) are removed; at this time, since F has a dependency on the vertex D, G has a dependency on the vertex A, so it does not handle F and G.

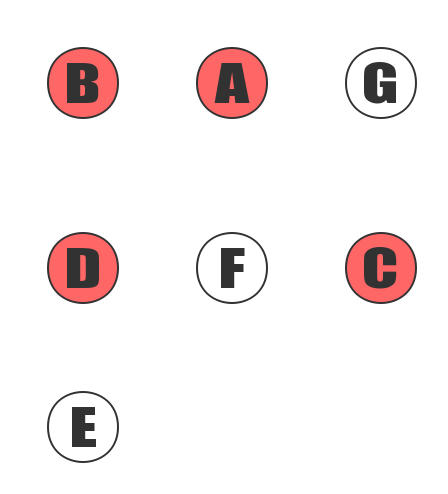
  2. A, D is added to the sorting result in turn.

    After the first step, both A and D are not dependent on the vertex, accessing the A first and then accessing the D according to the storage order. After the access, the edges of the vertex A and the vertex D are deleted.

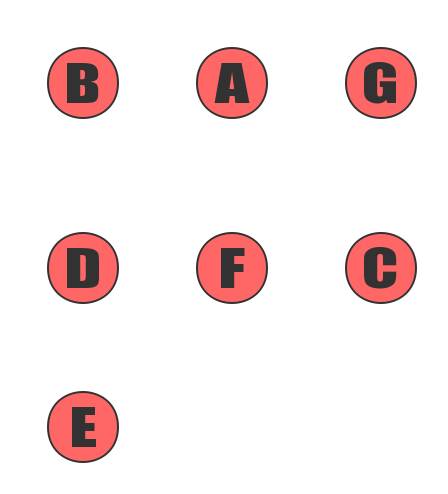
  3. Add E, F, G to the sorting result.

C++ Implementation

Adjacency Matrix Version
1
// Work in progress
Adjacency List Version
1
// Work in progress
Share