N-Queens Problem

 |  WORDS: 394 | Time: 2 Mins
AlgorithmProblems
Algorithm, Backtracking, C++

N-Queens Problem

Overview

The eight queens problem is a question with chess as the background: how to place eight queens on an 8×8 chess board so that no queen can directly eat other queens? In order to achieve this purpose, any two queens are not in the same horizontal, vertical or diagonal. The eight queen problem can be extended to the more general N-Queens Problem.

more information about n-queens problem please google it.

C++ Code

1
2
3
4
5
6
7
8
9
10
11
12
int NQueens(int n) {
    int upperlim = (1 << n) - 1, sum = 0;
    std::function<void(int,int,int)> dfs = [&](int row,int ld,int rd) {
        if(row == upperlim) {++sum;return;}
        for(int cur = upperlim & (~(row|ld|rd)),pos = 0;cur ;dfs(row|pos,(ld|pos)<<1,(rd|pos)>>1)) {
            pos = cur & (-cur);
            cur -= pos;
        }
    };
    dfs(0,0,0);
    return sum;
}

Introduction

initialization

1
upperlim = (1 << n) - 1, sum = 0;

Upperlim value is n-bit binary 1.

Recursive Function

1
2
3
4
5
6
7
std::function<void(int,int,int)> dfs = [&](int row,int ld,int rd) {
    if(row == upperlim) {++sum;return;}
    for(int cur = upperlim & (~(row|ld|rd)),pos = 0;cur ;dfs(row|pos,(ld|pos)<<1,(rd|pos)>>1)) {
        pos = cur & (-cur);
        cur -= pos;
    }
};

The function has three parameters:

  • row : row
  • ld : Left diagonal
  • rd : Right diagonal

Use these three parameters to determine whether a queen can be placed in a certain position.

Diagram

Here is a step-by-step illustration of the Six Queens question.

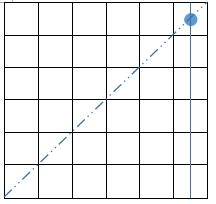
Step #1

1
2
3
4
5
row = 000001
ld  = 000010
rd  = 000000
cur = 111100
pos = 000100

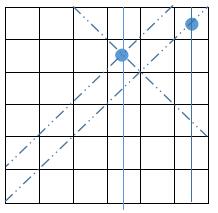
Step #2

1
2
3
4
5
row = 000101
ld  = 001100
rd  = 000010 
cur = 110000
pos = 010000

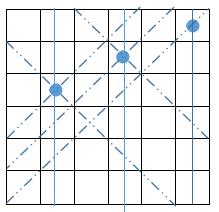
Step #3

1
2
3
4
5
row = 010101
ld  = 111000
rd  = 001001 
cur = 000010
pos = 000010

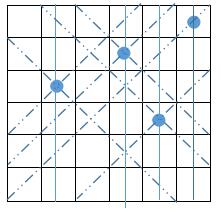
Step #4

1
2
3
4
5
row = 010111
ld  = 110100
rd  = 000101 
cur = 001000
pos = 001000

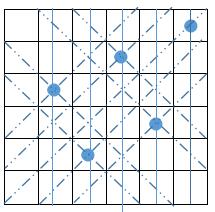
Step #5

1
2
3
4
5
row = 011111
ld  = 111000
rd  = 000110
cur = 000000
pos = 000000

The first round of search is completed, there is a kind of thought is the depth first search, is to find a solution and then press forward to the enemy’s capital to find second solution, because the eight queens problem belongs to the scope of the graph, so the idea of graph theory can be found in this problem.

Share