Various surfaces

Ray-Plane Intersection

Plane is often represented in implicit form :

$$Ax + By + Cz + D = 0$$

Equivalent:

$$N \cdot P + D = 0$$

where $N = [A B C]^T$ and $P = [x y z]^T$

To find ray-plane intersection, substitute ray equation $P(t)$ into plane equation:

1. We get $N \cdot P + D = 0$.
2. Sovle for $t$ to get $t_0$.
3. if $t_0$ is infinity, no intersection (ray is parallel to plane).
4. Intersection point is $P(t_0)$.
5. Verify that intersection is not behind ray origin.

The normal at the intersection is $N$ (or $-N$)

bool Plane::hit( const Ray &r, double tmin, double tmax, SurfaceHitRecord &rec ) const 
{
	Vector3d N( A, B, C );
	double NRd = dot( N, r.direction() );
	double NRo = dot( N, r.origin() );
	double t = (-D - NRo) / NRd;
	if ( t < tmin || t > tmax ) 
	{
		return false;
	}
	rec.t = t;
	rec.p = r.pointAtParam(t);
	rec.normal = N;
	rec.mat_ptr = matp;
	return true;
}

Ray-Sphere Intersection

Sphere (centered at origin) is often represented in implicit form:

$$x^2 + y^2 + z^2 - r^2 = 0$$

Equivalent:

$$P \cdot P - r^2 = 0$$

To find ray-plane intersection, substitute ray equation P(t) into plane equation:

We get $P \cdot P - r^2 = 0$:

$$P(t) \cdot P(t) - r^2 = 0$$ $$(R_o + tR_d) \cdot (R_o + tR_d) - r^2 = 0$$ $$R_d \cdot R_dt^2 + 2R_d \cdot R_o + R_o \cdot R_o - r^2 = 0$$

$R_o$ is ray origin, $R_d$ is ray direction.

It is a quadratic equation in the form $at^2 + bt + c = 0$

• $a = R_o \cdot R_o = 1$ (Since $|R_d| = 1$)
• $b = 2R_d \cdot R_o$
• $c = R_o \cdot R_o - r^2$

Discriminant: $d = b^2 + 4ac$

Solution: $t_\pm = \frac{-b\pm\sqrt{b^2 + 4ac}}{2a}$

Choose $t_0$ as the closest positive $t$ value ($t_+$ + or $t_-$)

The normal at the intersection point is $P(t_0)/|P(t_0)|$

Very easy to compute, that is why most ray tracing images have spheres.

bool Sphere::hit( const Ray &r, double tmin, double tmax, SurfaceHitRecord &rec ) const 
{
    Vector3d Rd = r.direction();
    Vector3d Ro = r.origin() - center;
    double a = dot(Rd,Rd);
    double b = 2.0 * dot(Rd, Ro);
    double c = dot(Ro,Ro) - pow(radius, 2);
    double d = pow(b, 2) - 4.0 * a * c;
    if(d < 0)
    {
        return false;
    }
    double t = (-b - sqrt(d)) / (2.0f * a);
    if ( t >= tmin && t <= tmax )
    {
        rec.t = t ;
        rec.p = r.pointAtParam(t);
        rec.normal = (Ro + t * Rd) / radius;
        rec.mat_ptr = matp;
        return true;
    }
    return false;
}

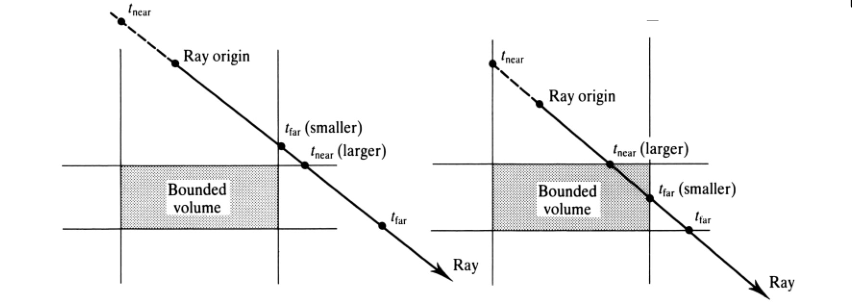
Ray-Box Intersection

To find ray-box intersection:

• For each pair of parallel plane, find the distance to the first plane ($t_{near}$) and to the second plane ($t_{far}$).
• Keep the largest $t_{near}$ so far, and smallest $t_{far}$ so far.
• If largest $t_{near}$ > smallest $t_{far}$ , no intersection.
• Otherwise, the intersection is at P(largest $t_{near}$ )

Ray-Triangle Intersection

Finding intersection between a ray and a general polygon is difficult.

• Compute ray-plane intersection
• Determine whether intersection is within polygon
  • Tedious for non-convex polygon
• Interpolation of attributes at the vertices are not well-
  defined

Much easier to find ray-triangle intersection

• Can use the barycentric coordinates method.
• Interpolation of attributes at the vertices are well-defined using the barycentric coordinates.

bool Triangle::hit( const Ray &r, double tmin, double tmax, SurfaceHitRecord &rec ) const 
{
	double A = v0.x() - v1.x();
	double B = v0.y() - v1.y();
	double C = v0.z() - v1.z();

	double D = v0.x() - v2.x();
	double E = v0.y() - v2.y();
	double F = v0.z() - v2.z();

	double G = r.direction().x();
	double H = r.direction().y();
	double I = r.direction().z();

	double J = v0.x() - r.origin().x();
	double K = v0.y() - r.origin().y();
	double L = v0.z() - r.origin().z();

	double EIHF = E*I - H*F;
	double GFDI = G*F - D*I;
	double DHEG = D*H - E*G;

	double denom = (A*EIHF + B*GFDI + C*DHEG);

	double beta = (J*EIHF + K*GFDI + L*DHEG) / denom;

	if ( beta < 0.0 || beta > 1.0 ) return false;

	double AKJB = A*K - J*B;
	double JCAL = J*C - A*L;
	double BLKC = B*L - K*C;

	double gamma = (I*AKJB + H*JCAL + G*BLKC) / denom;

	if ( gamma < 0.0 || beta + gamma > 1.0 ) return false;

	double t = -(F*AKJB + E*JCAL + D*BLKC) / denom;

	if ( t >= tmin && t <= tmax )
	{
		// We have a hit -- populat hit record. 
		rec.t = t;
		rec.p = r.pointAtParam(t);
		double alpha = 1.0 - beta - gamma;
		rec.normal = alpha * n0 + beta * n1 + gamma * n2;
		rec.mat_ptr = matp;
		return true;
	}
	return false;
}

Barycentric Coordinates

The barycentric coordinates of a point P on a triangle $ABC$ is ($ \alpha $, $ \beta $, $ \gamma $) such that:

$$P = \alpha A + \beta B + \gamma C$$

where

$$\alpha + \beta + \gamma = 1$$

and

$$0 \leq \alpha,\beta,\gamma \leq 1$$

We can rewrite it as:

$$P = (1 - \beta - \gamma)A + \beta B + \gamma C$$ $$P = A + \beta(B-A) + \gamma(C-A)$$

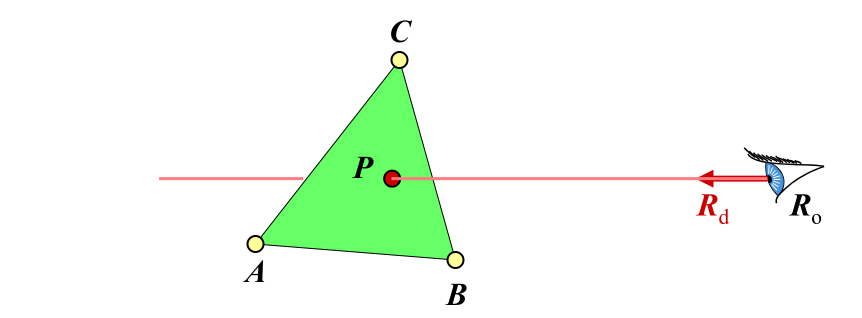
To find ray-triangle intersection, we let:

$$P(t) = A + \beta(B-A) + \gamma(C-A)$$ $$R_o + tR_d = A + \beta(B-A) + \gamma(C-A)$$

Solve for $t$, $\beta$ and $\gamma$

Intersection if $\beta + \gamma < 1$ and $\beta,\gamma > 0$ and $t > 0$

Expand &R_o + tR_d = A + \beta(B-A) + \gamma(C-A)&

$$\begin{cases} R_{ox} + tR_{dx} = A_x + \beta(B_x-A_x) + \gamma(C_x + A_x) \\ R_{oy} + tR_{dy} = A_y + \beta(B_y-A_y) + \gamma(C_y + A_y) \\ R_{oz} + tR_{dz} = A_z + \beta(B_z-A_z) + \gamma(C_z + A_z) \\ \end{cases}$$

we have 3 equations and 3 unknowns here.

Regroup and write in matrix form

$$\begin{bmatrix} A_x - B_x &A_x - C_x &R_{dx}\\ A_y - B_y &A_y - C_y &R_{dy}\\ A_z - B_z &A_z - C_z &R_{dz} \end{bmatrix} \begin{bmatrix} \beta \\ \gamma \\ t \end{bmatrix} = \begin{bmatrix} A_x - R_{ox} \\ A_y - R_{oy} \\ A_z - R_{oz} \end{bmatrix}$$

Use Cramer’s Rule to solve for $t$, $\beta$ and $\gamma$

$$\beta = \frac { \begin{vmatrix} A_x - R_{ox} &A_x-C_x &R_{dx} \\ A_y - R_{oy} &A_y-C_y &R_{dy} \\ A_z - R_{oz} &A_z-C_z &R_{dz} \end{vmatrix} } { |A| }$$ $$\gamma = \frac { \begin{vmatrix} A_x - B_{x} &A_x-R_{ox} &R_{dx} \\ A_y - B_{y} &A_y-R_{oy} &R_{dy} \\ A_z - B_{z} &A_z-R_{oz} &R_{dz} \end{vmatrix} } { |A| }$$ $$t= \frac { \begin{vmatrix} A_x - B_{x} &A_x - C_{x} &A_x-R_{ox} \\ A_y - B_{y} &A_x - C_{x} &A_y-R_{oy} \\ A_z - B_{z} &A_x - C_{x} &A_z-R_{oz} \end{vmatrix} } { |A| }$$

bool Triangle::hit( const Ray &r, double tmin, double tmax, SurfaceHitRecord &rec ) const 
{	
    Vector3d e1 = v1 - v0;
	Vector3d e2 = v2 - v0;
	Vector3d p = cross( r.direction(), e2 );	
	double a = dot( e1, p );
    double f = 1.0 / a;
	Vector3d s = r.origin() - v0;
	double beta = f * dot( s, p );
    if ( beta < 0.0 || beta > 1.0 ) 
	{
		return false;
	}

	Vector3d q = cross( s, e1 );
    double gamma = f * dot( r.direction(), q );
    if ( gamma < 0.0 || beta + gamma > 1.0 ) 
	{
		return false;
	}

    double t = f * dot( e2, q );

	if ( t >= tmin && t <= tmax )
	{
		rec.t = t;
		rec.p = r.pointAtParam(t);
		double alpha = 1.0 - beta - gamma;
		rec.normal = alpha * n0 + beta * n1 + gamma * n2;
		rec.mat_ptr = matp;
		return true;
	}
	return false;
}

Advantages of Barycentric Intersection

• Efficient
• No need to store plane equation
• Barycentric coordinates are useful for linear interpolation of normal vectors, texture coordinates, and other attributes at the vertices

For example, the interpolated normal at $P$ is:

$$N_p = (1 - \beta - \gamma)N_A + \beta N_B + \gamma N_C$$

and all vector should do a normalization.

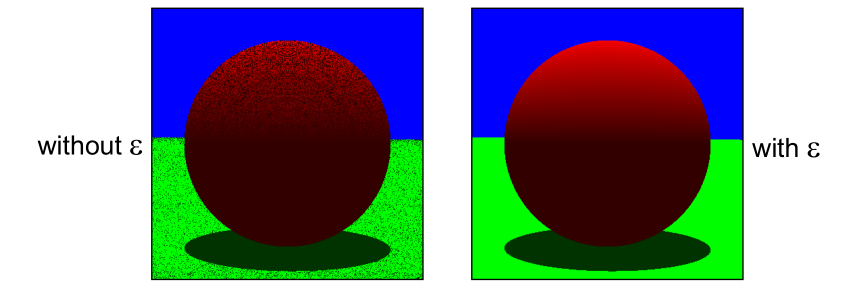
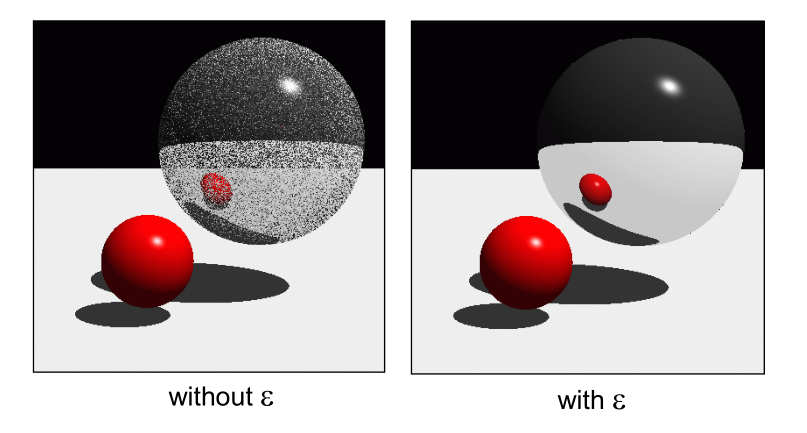
The “Epsilon” Problem

Should not accept intersection for very small positive $t$

• May falsely intersect the surface at the ray origin
• Method 1: Use an epsilon value $\varepsilon$ > 0, and accept an intersection only if its $t > \varepsilon$.
• Method 2: When a new ray is spawned, advanced the ray origin by an epsilon distance $\varepsilon$ in the ray direction

Reference

Learn OpenGL