RedBlackTree_II

 |  WORDS: 1,119 | Time: 7 Mins
Data StructureTree
C++, Data Structure, Tree

RedBlackTree II Chinese version address

The Last Section

Basic operation of red black trees

Insert

Insert a node into the red-black tree, which steps need to be performed?

  1. think of the red-black tree as a binary search tree and insert the node.
  2. Set this node to red.
  3. Modify the tree by rotating and recoloring it to make it a red-black tree again.

Step Description

Step 1

The red-black tree is a binary search tree, which is still a binary search tree after the node is inserted. This means that the key of the tree is still ordered. In addition, whether it is left-rotation or right-rotation, the tree is a binary search tree before rotation, and after rotation it must be a binary search tree.

Step 2

Why should set the node’s color to red?

Because it is not violate 5 features. violate more less feature mean less things we need to deal with.

Step 3

So how many features it violate?

  1. As for feature 1, obviously not violate.
  2. As for feature 2, insert operation does not change the root node, so the color of root node is still black.
  3. As for feature 3, leaf node is null node, inserting non-null node does not affect feature.
  4. As for feature 4, Is possible to violate.

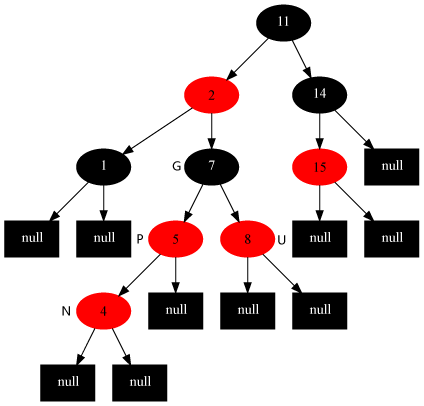
Case Description

Case 1
Description

The current node’s parent node is red, and the current node’s grandparent node’s other child node (uncle node) is also red

1
2
3
4
while color[p[z]] = RED                                                  
    do if p[z] = left[p[p[z]]]                                           
          then y ← right[p[p[z]]]                                       
               if color[y] = RED

Grandfather node must exist at this time, otherwise it is not black red tree before inserting. At this point is divided into the parent node is the grandfather’s left child or right child, according to symmetry, we just untie a direction on it. Here only consider the parent node left grandfather’s situation, as shown below.

Method

Strategy is as follows:

  1. Sets the parent node to black.
  2. Sets the node of the uncle to black.
  3. set grandfather node to red.
  4. The grandfather node is set as the current node (red node).

As shown in the following pseudo code:

1
2
3
4
then color[p[z]] ← BLACK                  ▹ Case 1   
   color[y] ← BLACK                       ▹ Case 1   
   color[p[p[z]]] ← RED                   ▹ Case 1   
   z ← p[p[z]]                            ▹ Case 1

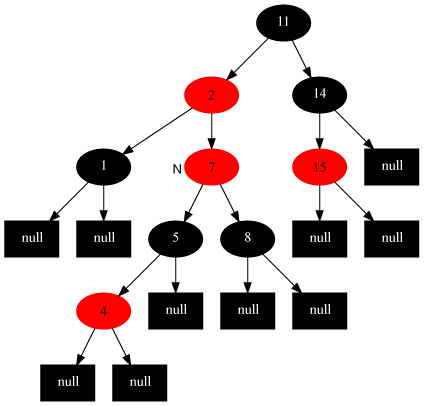
Then, insert repair case 1 translates into insert repair case 2.

Case 2
Description

The current node’s parent node is red, the uncle node is black, and the current node is the right child of its parent node

Method

Strategy is as follows:

  1. Set the parent as the new current node.
  2. Do left rotation on current node.

As shown in the following pseudo code:

1
2
3
else if z = right[p[z]]                                
      then z ← p[z]                       ▹ Case 2   
           LEFT-ROTATE(T, z)              ▹ Case 2

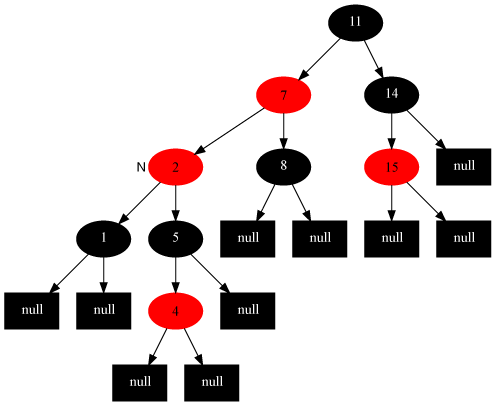
Insertion Repair Case 2 translates into insert repair case 3.

Case 3
Description

The current node’s parent node is red, the uncle node is black, and the current node is the left child of its parent node

Method

Strategy is as follows:

  1. Sets the parent node to black.
  2. set grandfather node to red.
  3. Do right rotation on grandfather node.

As shown in the following pseudo code:

1
2
3
color[p[z]] ← BLACK                 ▹ Case 3   
color[p[p[z]]] ← RED                ▹ Case 3   
RIGHT-ROTATE(T, p[p[z]])            ▹ Case 3

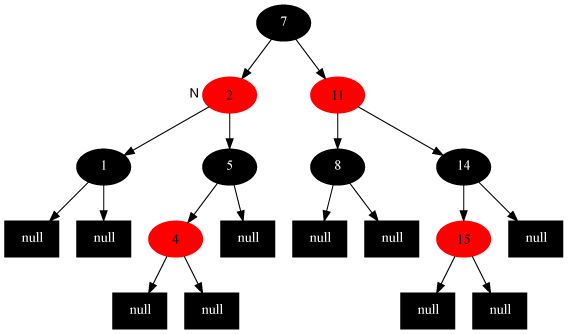
Code Reference

Pseudo code:

Insert Pseudo Code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
RB-INSERT(T, z)  
 y ← nil[T]                        
 x ← root[T]                       
 while x ≠ nil[T]                  
     do y ← x                      
        if key[z] < key[x]  
           then x ← left[x]  
           else x ← right[x]  
 p[z] ← y                          
 if y = nil[T]                     
    then root[T] ← z               
    else if key[z] < key[y]        
            then left[y] ← z       
            else right[y] ← z       
 left[z] ← nil[T]                  
 right[z] ← nil[T]                 
 color[z] ← RED                    
 RB-INSERT-FIXUP(T, z)
Insert-Fixed Pseudo Code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
RB-INSERT-FIXUP(T, z)
while color[p[z]] = RED                                                  
    do if p[z] = left[p[p[z]]]                                           
          then y ← right[p[p[z]]]                                       
               if color[y] = RED                                         
                  then color[p[z]] ← BLACK                    ▹ Case 1   
                       color[y] ← BLACK                       ▹ Case 1   
                       color[p[p[z]]] ← RED                   ▹ Case 1   
                       z ← p[p[z]]                            ▹ Case 1   
                  else if z = right[p[z]]                                
                          then z ← p[z]                       ▹ Case 2   
                               LEFT-ROTATE(T, z)              ▹ Case 2   
                          color[p[z]] ← BLACK                 ▹ Case 3   
                          color[p[p[z]]] ← RED                ▹ Case 3   
                          RIGHT-ROTATE(T, p[p[z]])            ▹ Case 3  
       else (same as then clause with "right" and "left" exchanged)      
color[root[T]] ← BLACK

C++ Implementation

Insert C++ Code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
template <class T>
bool RedBlackTree<T>::insert(RedBlackNode<T> *&root, RedBlackNode<T> *node) {

	RedBlackNode<T>* y = nullptr;   
	RedBlackNode<T>* x = root;     

	while (x != nullptr) {          

		if(x->key == node->key){    
			return false;
		}

		y = x;                     
		if(node->key < x->key) {   
			x = x->pLeft;           
		} else {
			x = x->pRight;			
		}

	}

	
	node->pParent = y;				

	if(y != nullptr) {				
		if(node->key < y->key) {	
			y->pLeft = node;		
		} else {					
			y->pRight = node;		
		}
	} else {
		root = node;				
	}

	set_red(node);		

	insertFixUp(root, node);

	return true;

}
Insert-Fixed C++ Code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
template <class T>
void RedBlackTree<T>::insertFixUp(RedBlackNode<T> *&root, RedBlackNode<T> *node) {

	RedBlackNode<T>* parent;
	RedBlackNode<T>* gparnet;

	while ((parent = get_parent(node))&&(is_red(parent))) {

		gparnet = get_parent(parent);

		if(parent == gparnet->pLeft) {
            RedBlackNode<T>* uncle = gparnet->pRight;
            if(uncle && is_red(uncle)) {
                set_black(uncle);
                set_black(parent);
                set_red(gparnet);
                node = gparnet;
                continue;
            }
            if(parent->pRight == node) {
                RedBlackNode<T>* tmp;
                leftRotate(root, parent);
                tmp = parent;
                parent = node;
                node = tmp;
            }
            set_black(parent);
            set_red(gparnet);
            rightRotate(root, gparnet);

		}
		else {
            RedBlackNode<T>* uncle = gparnet->pLeft;
            if(uncle && is_red(uncle)) {
                set_black(uncle);
                set_black(parent);
                set_red(gparnet);
                node = gparnet;
                continue;
            }
            if(parent->pLeft == node) {
                RedBlackNode<T>* tmp;
                rightRotate(root, parent);
                tmp = parent;
                parent = node;
                node = tmp;
            }
            set_black(parent);
            set_red(gparnet);
            leftRotate(root, gparnet);
        }

	}
	set_black(root);
}

The Next Section

Share